Teknik Berhitung Cepat Akar (Irasional)
Membuat soal matematika tidak semudah yang dibayangkan. Tidak cukup sekedar membuat sebarang soal. Tujuan membuat soal itu haruslah jelas. Kepada siapa soal itu ditujukan juga harus jelas sejak awal.
Saya menemukan beberapa guru yang baik kesulitan membuat soal yang berhubungan dengan akar kuadrat (atau akar kubik). Tetapi guru yang kurang baik justru sering merasa tidak ada masalah dalam membuat atau menyusun soal tentang akar kuadrat.
Misal, untuk anak SD (sekitar kelas 5) mulai mengenal konsep kuadrat atau akar. Tentu seorang siswa tidak akan sulit memahami bahwa akar 9 adalah 3. Karena para siswa sudah paham dengan akar 9, guru mencoba memberi soal yang lebih mudah:
Berapakah akar 8?
Berapakah akar 3?
Berapakah akar 2?
Apanya yang lebih mudah?
Bilangan lebih kecil tidak secara otomatis menjadi lebih mudah. Saya telah mengembangkan banyak cara untuk menghitung akar kuadrat yang mudah dan menyenangkan di matematika kreatif APIQ. Lebih-lebih untuk menghitung akar pangkat tiga (akar kubik), siswa-siswa APIQ sangat menyukainya.
Tentu saya dengan sengaja dari awal telah memisahkan antara akar rasional dan akar irasional. Orang sering terjebak memaksa diri agar bisa menghitung akar rasional dan irasional dengan sebuah metode yang sama. Menurut pengalaman saya, akan lebih mudah bila kita memisahkan dua hal di atas.
Untuk menghitung akar irasional, saya mencoba mengembangkan berbagai macam cara:
1. Teknik Bintang Aritmetika; teknik ini menurut saya bagus. Tetapi tidak selalu mudah untuk melakukannya. Secara prinsip cara ini adalah menghitung akar dengan cara membalik algoritma menghitung kuadrat.
2. Teknik Pecahan Tak Hingga; inilah teknik yang saya sukai. Bentuknya cantik dan (tampak) sederhana. Pertama, kita perlu tahu bagaimana mengubah bentuk akar ke bentuk pecahan. Lalu menghitung pecahan tersebut.
3. Menggunakan program komputer; tentu ini metode yang ampuh. Bagi Anda yang menyukai pemrogramman komputer silakan mencobanya dengan berbagai macam alternatif algoritma pemrogramman.
Saya berniat eksperimen dan sharing cara menghitung akar kuadrat ini dalam forum Training APIQ Quantum yang akan kami selenggarakan 23-24 Mei 2009 di Jakarta. Selamat berpartisipasi…!
Salam hangat…
(angger; agus Nggermanto: Pendiri APIQ)
*Ngomong-ngomong akar 2 adalah = 1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799….
Saya menemukan beberapa guru yang baik kesulitan membuat soal yang berhubungan dengan akar kuadrat (atau akar kubik). Tetapi guru yang kurang baik justru sering merasa tidak ada masalah dalam membuat atau menyusun soal tentang akar kuadrat.
Misal, untuk anak SD (sekitar kelas 5) mulai mengenal konsep kuadrat atau akar. Tentu seorang siswa tidak akan sulit memahami bahwa akar 9 adalah 3. Karena para siswa sudah paham dengan akar 9, guru mencoba memberi soal yang lebih mudah:
Berapakah akar 8?
Berapakah akar 3?
Berapakah akar 2?
Apanya yang lebih mudah?
Bilangan lebih kecil tidak secara otomatis menjadi lebih mudah. Saya telah mengembangkan banyak cara untuk menghitung akar kuadrat yang mudah dan menyenangkan di matematika kreatif APIQ. Lebih-lebih untuk menghitung akar pangkat tiga (akar kubik), siswa-siswa APIQ sangat menyukainya.
Tentu saya dengan sengaja dari awal telah memisahkan antara akar rasional dan akar irasional. Orang sering terjebak memaksa diri agar bisa menghitung akar rasional dan irasional dengan sebuah metode yang sama. Menurut pengalaman saya, akan lebih mudah bila kita memisahkan dua hal di atas.
Untuk menghitung akar irasional, saya mencoba mengembangkan berbagai macam cara:
1. Teknik Bintang Aritmetika; teknik ini menurut saya bagus. Tetapi tidak selalu mudah untuk melakukannya. Secara prinsip cara ini adalah menghitung akar dengan cara membalik algoritma menghitung kuadrat.
2. Teknik Pecahan Tak Hingga; inilah teknik yang saya sukai. Bentuknya cantik dan (tampak) sederhana. Pertama, kita perlu tahu bagaimana mengubah bentuk akar ke bentuk pecahan. Lalu menghitung pecahan tersebut.
3. Menggunakan program komputer; tentu ini metode yang ampuh. Bagi Anda yang menyukai pemrogramman komputer silakan mencobanya dengan berbagai macam alternatif algoritma pemrogramman.
Saya berniat eksperimen dan sharing cara menghitung akar kuadrat ini dalam forum Training APIQ Quantum yang akan kami selenggarakan 23-24 Mei 2009 di Jakarta. Selamat berpartisipasi…!
Salam hangat…
(angger; agus Nggermanto: Pendiri APIQ)
*Ngomong-ngomong akar 2 adalah = 1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799….



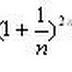
0 comments:
Post a Comment